Hace tiempo hice un post acerca de cómo mejorar las lecturas analógicas de tu Arduino. Hoy os traigo la parte 2, en la cual añado nuevos métodos para mejorar las lecturas. En este post me centraré en los ajustes de VREF, y en una nueva funcionalidad que le he añadido a la librería que hice con este propósito.
Arduino ajustando el VREF
Algunos microcontroladores como Arduino, utilizan por norma la fuente de alimentación como referencia para los ADC. Esto en el laboratorio es muy cómodo y suele funcionar bien, pero en la vida real puede dar problemas.
Por poner un ejemplo, en el cálculo ADC solemos tomar como referencia los 5v de alimentación de Arduino. Esto es un problema, porque la fuente de alimentación quizá esté entregando 5.1v o 4.9v. Teniendo en cuenta esto, tus mediciones Analógicas serán imprecisas.
También se puede dar el caso de que alimentes tu Arduino con baterías, las cuales dan como mucho 4.2v y pueden bajar hasta 3v. Según vaya cayendo el voltaje, las mediciones se volverán más imprecisas.
¿Cómo solucionamos esto?
Si quieres mejorar las lecturas analógicas de Arduino, puedes usar el pin VREF por ejemplo. Este pin nos permite introducir un voltaje de referencia a nuestro gusto para calibrar el ADC. Si prevemos que el voltaje puede caer hasta 3v, puedes poner un regulador LDO de 2v en el pin VREF. Con ello, podrás usar este voltaje de referencia en tus medidas ADC y será preciso independientemente de si el voltaje de alimentación varía.
Para usar el pin VREF para tus mediciones en Arduino, tendrías que poner la siguiente línea en el bloque setup de tu proyecto:
analogReference(EXTERNAL);
Otra posibilidad que nos brinda Arduino, es utilizar la referencia interna del microcontrolador. Este voltaje es de 1.1v y es fijo independientemente del voltaje exterior, por lo que es una referencia estable. Para activarlo podemos poner la siguiente línea en el bloque setup de nuestro proyecto:
analogReference(INTERNAL);
Otros microcontroladores como el Arduino Mega también proveen de una referencia interna de 2.56v. Si quieres más información, puedes pasarte por la documentación de Arduino.
Es muy importante que al calcular tus mediciones ADC utilices el voltaje de referencia en tus cálculos. El rango de medición será siempre desde 0 a 1023, independientemente del voltaje de referencia. Así para una referencia de 1.1v, 0.55v darán como resultado 512, mientras que para una referencia de 5v será de aproximadamente 112.
Cómo mejorar las lecturas analógicas
Ya os he hablado de cómo mejorar la precisión ajustando el VREF. Es muy importante ya que sin una referencia buena las mediciones serán incorrectas siempre. Hecho esto, ahora toca ver la parte de reducir el error por las fluctuaciones eléctricas. El pin ADC siempre estará sujeto a interferencias, por lo que las mediciones ADC rara vez serán estables. Para estabilizarlas podemos utilizar varios métodos, pero yo aquí hablaré del método por condensador, y a través de cálculos matemáticos.
Usando un condensador
Los condensadores son usados para reducir las fluctuaciones en la tensión en las fuentes de alimentación. Qué componente mejor que este podemos usar para nuestro propósito. Poniendo simplemente un condensador de 0.1uf entre masa y el pin ADC que vamos a usar, ayudaremos a eliminar los picos indeseados en las mediciones.
Usando las matemáticas para mejorar las lecturas analógicas
Las matemáticas son nuestras amigas en multitud de ocasiones, y esta no va a ser una menos. Para mejorar las lecturas analógicas hay distintos métodos, pero yo hablaré de la media básica, y la media móvil exponencial. Estos dos métodos son simples y muy útiles.
Media básica
La media básica como su nombre indica, es el método básico de sacar la media de una serie de números. Para ello, sumamos X números, y dividimos el total entre la cantidad de números. Esta media basa su precisión en la cantidad de números que usemos, así si por ejemplo usamos 4 y hay un pico en uno de ellos, será más imprecisa que si usamos 10.
Esto son matemáticas, así que pongámosle números. Supongamos el caso de los cuatro números y que en uno hay un pico:
media = (n1 + n2 + n3 + n4) / 4
Si por poner un ejemplo n2 sufre de una interferencia y recibimos un pico en la medición, el resultado será el siguiente:
media = (123 + 220 + 125 + 121 ) / 4 = ~147
Ahí se ve claramente que la media debería rondar los 121-125, pero al haber recibido un pico en una de las mediciones perdemos precisión y nos sale muy alta. Si en lugar de usar 4 mediciones, usamos 10 y recibimos un pico, este problema se atenuará, por lo que cuantas más mediciones usemos en la media, más precisa será esta.
media = (123 + 220 + 125 + 121 + 120 + 127 + 123 + 121 + 125 + 120) / 10 = ~132
Como veis, la precisión sigue siendo un poco baja pero se acerca más a la realidad.
Media móvil exponencial
Como habrás observado, la media básica es un poco imprecisa y vulnerable a picos en las mediciones. Dependes de hacer muchas mediciones para sacar una media más precisa. Es por ello, que para mejorar este problema podemos utilizar fórmulas un poco más complejas y que reducen este error. Una de ellas es la media móvil exponencial, y su fórmula es:
media = (alfa * medición2) + ((1 - alfa) * medida1)
En esta fórmula, alfa es un número float entre 0 y 1, siendo lo más usado 0,05 o 0,1.
Si analizamos la fórmula, es bastante simple. Cogemos la nueva medición (medición2), y la multiplicamos por alfa, por lo que sacamos un porcentaje de ella (0,05 = 5%). Luego sumamos esta cantidad al porcentaje restante (1 – 0,05 = 0,95 = 95%), de la medición antigua (medición1). Con esto conseguimos que sólo una parte de la medición nueva afecte al resultado final, y por supuesto, cuanto más alto sea alfa, más afectará. Normalmente como medición antigua utilizamos la media sacada del cálculo anterior.
Pongamos el ejemplo de los cuatro números de antes:
media = (220 * 0,05) + ((1 - 0,05) * 123) = 127,85 media = (125 * 0,05) + ((1 - 0,05) * 127,85) = 127,70 media = (121 * 0,05) + ((1 - 0,05) * 127,70) = 127,37 -> INT -> 127
Como puedes ver, aunque la media sigue saliendo un poco alta es mucho más precisa que la media básica, acercándose con 4 números más a la medición real que incluso la media básica de 10 números de antes. Este tipo de media ayuda a reducir la cantidad de fluctuaciones y tiene la ventaja de que no tienes que llevar un control de la cantidad de números usados como la básica. Con este simple código Python sacamos la media de los 10 números de arriba:
numbers = [123, 220, 125, 121, 120, 127, 123, 121, 125, 120]
alfa = 0.1
# Sacamos la primera media entre los dos primeros números
media = (alfa * numbers[1]) + ((1 - alfa) * numbers[0])
# Realizamos la media móvil exponencial usando el resto de números
for i in range(2, len(numbers)):
media = (alfa * numbers[i]) + ((1 - alfa) * media)
print(media)
Este ejemplo da como resultado 126, que se acerca incluso un poco más a la media real sin la fluctuación. Además, lo bueno es que nos permite ajustar como si de un potenciómetro se tratara, cuánto afecta la nueva medición a la media anterior a través de alfa. Así con un alfa de 0.1 conseguiremos una media de 127, la cual es un poco más alta porque el pico afecta más a la media.
Resumiendo, el alfa controla cómo de estable es la media. Cuanto más alto sea alfa, más fluctuará, por lo que dependiendo del uso se puede ajustar. Por ejemplo, para un higrómetro o un termómetro nos vendrá bien que este número sea bajo porque su variación es lenta y muy baja, pero para otros casos como por ejemplo medir el voltaje de algo conectado nos puede venir mejor subirlo para detectar los cambios antes. Para verlo mejor, aquí tenéis tres capturas de pantalla en las que veréis el valor real, y cómo sería con alfa es 0,05 y 0,2. En ellas tenéis las mediciones de un ADC flotante, las cuales variarán muy bruscamente debido a las interferencias al no tener nada conectado.
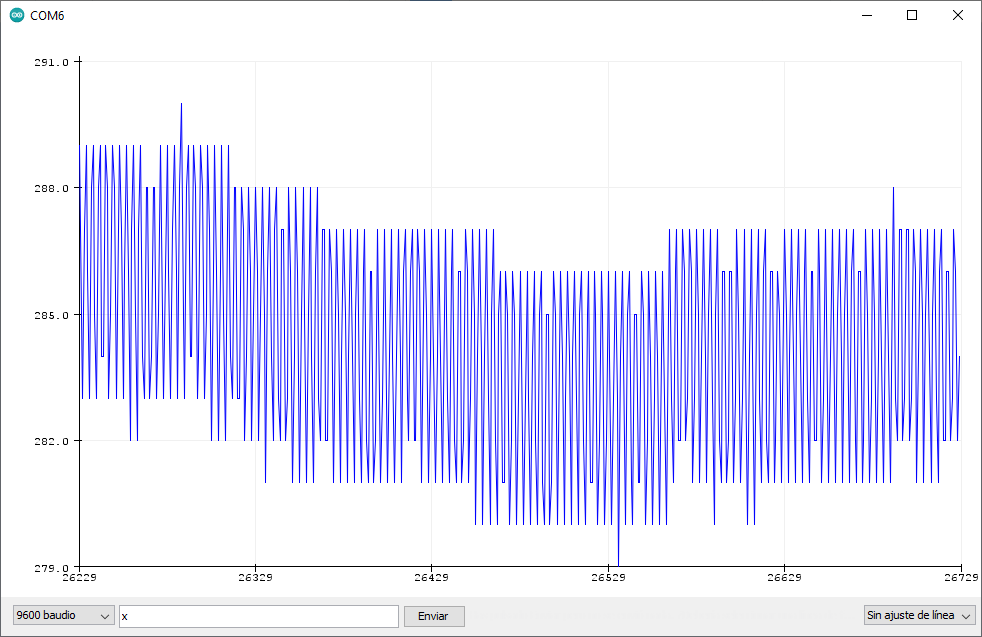
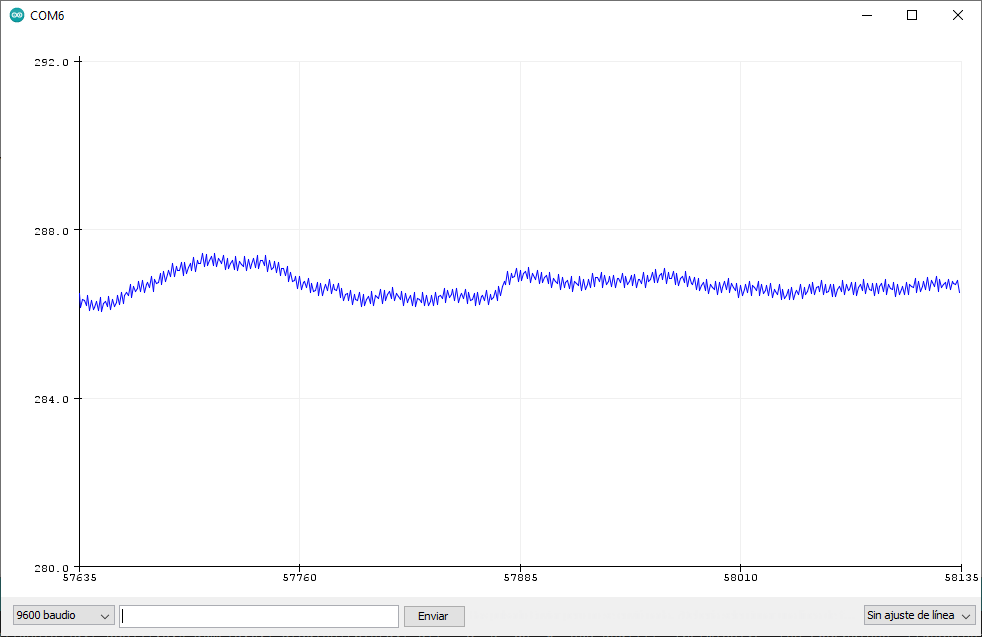
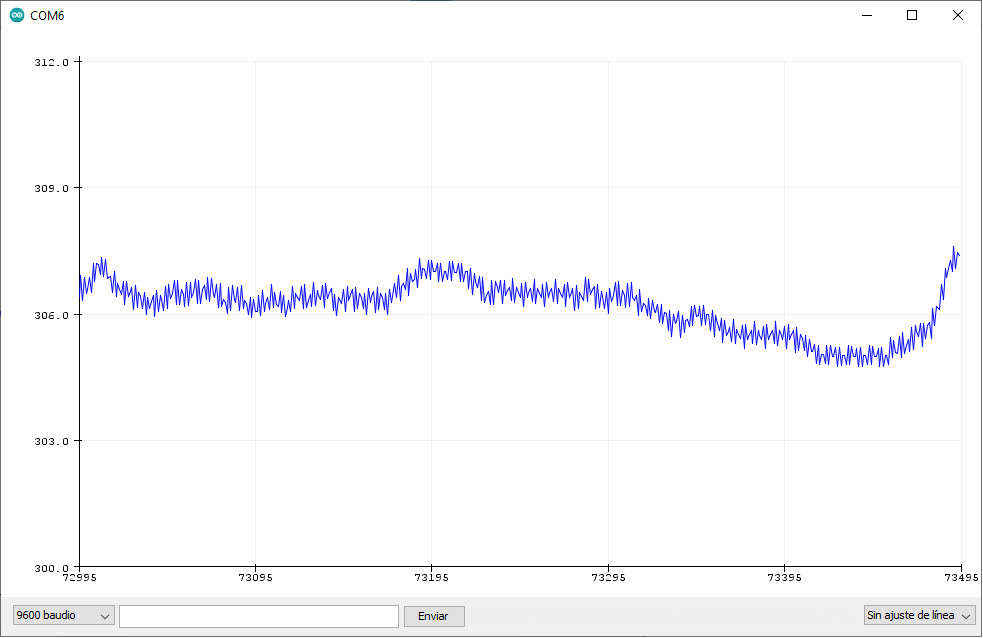
Como podéis observar, cuanto más alto es alfa, más se notan las fluctuaciones. Obviamente esto es un ejemplo exagerado y el ADC no debería fluctuar tanto. Tampoco hagáis caso al número de la última captura, el cual es superior a 300 mientras que los otros es de menos de 288. Por alguna razón subieron las interferencias mientras hacía la captura, pero lo verifiqué el valor y es correcto. Quizá alguien puso la lavadora por la zona…
Usar la librería
Arriba te hablé de que había creado una librería para este propósito, y sí, soy un poco cómodo. La función es simple y fácil de implementar, por lo que no necesita de librería. Qué se le va a hacer, soy así, me gusta tenerlo como librería para usarla siempre que quiera con dos simples métodos. Si tú también eres así de cómodo, puedes ver cómo descargar e instalar esta librería en la parte 1 de esta serie de posts.
Para usarla simplemente tienes que instalarla como indico en ese post, añadirla a tu sketch, inicializar el objeto y disfrutarla. Os pongo unas líneas de ejemplo con el ADC flotante para que hagáis vuestros experimentos:
#include <averager.h>
float alpha = 0.05;
averager<float> average;
void setup() {
Serial.begin(9600);
// Default is 0.1, so must be changed if we needs a different alpha
average.setExponentialMovingAverageAlpha(alpha);
}
void loop() {
uint16_t new_value = analogRead(A0);
average.updateExponentialMovingAverage(new_value);
Serial.println(average.getExponentialMovingAverage());
}
Un saludo y no dudéis en comentar las dudas o si simplemente queréis darme las gracias.
