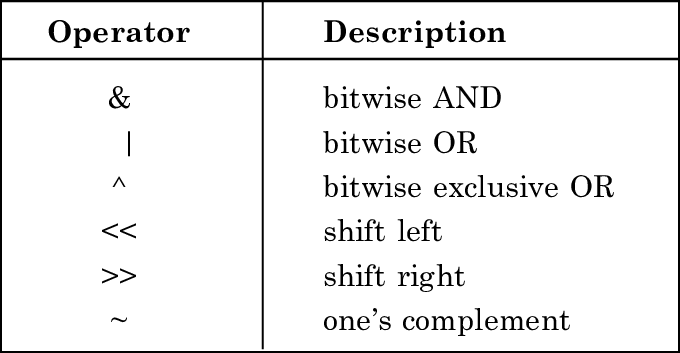
Hoy os traigo un pequeño tutorial acerca de cómo hacer operaciones bit a bit. Este tipo de operaciones siempre es útil conocerlas, ya que nos permitirán realizar operaciones como por ejemplo:
- Ahorrar memoria empaquetando varios boolean en un byte
- Trabajar con los registros del microcontrolador (de lo cual hablaré más adelante)
- Realizar operaciones aritméticas que incluyan multiplicar o dividir por potencias de 2
Aunque no me explayaré mucho ya que pretendo que sea un tutorial básico, intentaré que entiendas cómo realizarlas correctamente.
El sistema binario
Lo primero que debes entender es cómo funciona el sistema binario, ya que a partir de ahora indicaré todos los números en este sistema.
Un número binario es un número expresado en un sistema de base 2, el cual es utilizado en la electrónica digital. Esto significa que cada cifra indicada en este número puede ser 0 o 1 sólo.
En el sistema de numeración tradicional (base 10), un número puede decomponerse en potencias de base 10 de la siguiente manera:
684 = (6 * 102) + (8 + 101) + (4 * 100)
Al igual que el sistema de numeración tradicional, el binario se puede descomponer del mismo modo pero utilizando una base 2. Por supuesto hay que tener en cuenta que estos números sólo pueden ser 0 o 1.
45 = (1 * 25) + (0 * 24) + (1 * 23) + (1 * 22) + (0 * 21) + (1 * 20) = 101101
Es muy importante que entiendas cómo funciona el sistema binario para poder entender cómo realizar las operaciones con estos números.
En programación se suele usar 0b para indicar que el número es binario, por ejemplo 0b10 = 2. Por razones de compatibilidad, se mantiene el método para indicar el número binario con el prefijo B, por ejemplo B10 = 2.
Bitwise AND
El operador bitwise AND es un simple ampersand (&), usado entre dos números enteros. Este operador comparará bit a bit el número y dará como resultado 1 si ambos bits son 1, y 0 para el resto de posibilidades:
0 & 0 == 0 0 & 1 == 0 1 & 0 == 0 1 & 1 == 1
En programación, los números son almacenados en bits, por ejemplo un INT en Arduino contiene 16 bits. Utilizar este comparador en estos números realizará las operaciones AND bit a bit. Por ejemplo:
int a = 47; // 0000000000101111 int b = 75; // 0000000001001011 int c = a & b; // 0000000000001011 -> En decimal 11
Si te fijas en la última línea, el número es el resultado de la comparativa AND de las dos líneas superiores hecha bit a bit.
El uso más común del bitwise AND es seleccionar un bit concreto, dándonos como resultado el estado de dicho bit.
int x = 5; // binario: 101 int y = x & 1; // ahora y == 1 x = 4; // binario: 100 y = x & 1; // ahora y == 0
Bitwise OR
El operador bitwise OR se indica con una barra vertical | y al igual que el operador AND, realiza la comparación bit a bit. La diferencia es que en este caso el resultado será 1 si al menos uno de los dos bits es 1, y 0 sólo si ambos son 0.
0 | 0 == 0 0 | 1 == 1 1 | 0 == 1 1 | 1 == 1
Esto hará que el mismo ejemplo usado para el bitwise AND cambiando el operador, nos de un resultado bastante distinto:
int a = 47; // 0000000000101111 int b = 75; // 0000000001001011 int c = a | b; // 0000000001101111 -> En decimal 111
Este operador se suele utilizar para asegurarse de que un bit cambia a 1 sin modificar el resto, por ejemplo:
00101011 | 00000100 = 00101111 // Sólo modifica el tercer bit empezando por la derecha
Bitwise XOR
El operador XOR se indica con un símbolo de intercalado ^. Para no variar, este operador también realiza las operaciones bit a bit en los números. Su funcionamiento es similar al OR con la diferencia de que da 1 cuando los dos bits son distintos y 0 cuando son iguales:
0 ^ 0 == 0 0 ^ 1 == 1 1 ^ 0 == 1 1 ^ 1 == 0
Obviamente, el mismo ejemplo usado en los dos operadores anteriores nos dará un resultado distinto:
int a = 47; // 0000000000101111 int b = 75; // 0000000001001011 int c = a | b; // 0000000001100100 -> En decimal 100
Este operador es usado principalmente para alternar el estado de un bit, haciendo que un bit 0 se convierta a 1, y un bit 1 se convierta a 0:
00101011 | 00000110 = 00101101 // Alterna el estado del segundo y el tercer bit
Bitwise NOT
Este operador se indica con la tilde ~. Como seguramente habrás adivinado, este operador invierte los bits del número y al igual que el resto, realiza la operación bit a bit.
int a = 103; // binario: 0000000001100111 int b = ~a; // binario: 1111111110011000 = -104
Seguramente te llamará la atención que el número sea negativo. Eso es debido a que en las variables signed int (o simplemente int), el primer bit es el bit de signo por lo que si es 0 el número será positivo, y si es 1 será negativo (más información en la wikipedia). Esto obviamente no sucede con las variables de tipo unsigned int, ya que como el mismo nombre indica, carecen de signo.
Este bit de signo puede provocar sorpresas inesperadas, tal y como veremos más adelante.
Operadores Bit Shift
Los operadores Bit Shift son operadores que mueven los bits las posiciones que le indiquemos. Disponemos de dos operadores dependiendo de si queremos mover los bits a la izquierda (<<), o a la derecha (>>).
int a = 5; // binario: 0000000000000101 int b = a << 3; // binario: 0000000000101000, o 40 en decimal int c = b >> 3; // binario: 0000000000000101, vuelve a ser igual que a (5 en decimal)
Cuando mueves los bits hacia la izquierda, los bits del principio serán desterrados al olvido más absoluto. Una forma de entender más fácilmente este operador, es pensar que el número será multiplicado por 2 elevado al número de plazas que lo desplacemos:
1 << 0 == 1 1 << 1 == 2 1 << 2 == 4 1 << 3 == 8 ... 1 << 8 == 256 1 << 9 == 512 1 << 10 == 1024
En el caso de que muevas los bits a la derecha, el funcionamiento variará dependiendo del tipo de variable. Por poner un ejemplo, en un INT con un número negativo (el bit más alto a 1), provocará que dicho bit sea copiado en los bits más bajos.
int x = -16; // binario: 1111111111110000 int y = x >> 3; // binario: 1111111111111110
Este efecto llamado extensión de signo es muy probable que no sea lo que quieras. Para evitarlo, puedes aprovechar que el funcionamiento del shift hacia derecha es diferente en las variables unsigned int y hacer un casting de tipo para suprimir los 1 que se copian del principio:
int x = -16; // binario: 1111111111110000 int y = unsigned(x) >> 3; // binario: 0001111111111110
Si arriba te indiqué que el operador bit shift hacia la izquierda multiplicaba por 2 elevado al número de plazas a mover, el operador bit shift hacia la derecha se puede entender como lo contrario: dividir el número entre 2 elevado al número de plazas:
1024 >> 0 == 1024 1024 >> 1 == 512 1024 >> 2 == 256 1024 >> 3 == 128 ... 1024 >> 8 == 4 1024 >> 9 == 2 1024 >> 10 == 1
Operadores de asignación
Los operadores de asignación funcionan exactamente igual que los usados con las sumas, restas… Si no sabes de lo que estoy hablando, una operación aritmética sobre una variable se puede escribir de la siguiente manera:
int x = 2; int x = x + 3; // Sustituye x por el resultado de x + 3 (5)
Para abreviar, podemos realizar la misma operación de la siguiente manera:
int x = 2; int x += 3; // Hace exactamente lo mismo que el ejemplo de arriba
Este mismo método lo puedes utilizar para los operadores bitwise, salvo para el operador NOT, el cual no dispone de método abreviado:
int x = 1; // binario: 0000000000000001 x <<= 3; // binario: 0000000000001000 x |= 3; // binario: 0000000000001011 - porque 3 es 11 en binario x &= 1; // binario: 0000000000000001 x ^= 4; // binario: 0000000000000101 - Alterna usando la máscara de binario 100 x ^= 4; // binario: 0000000000000001 - Alterna de nuevo los bits dejándolos como antes
Tal y como te comenté, el operador NOT no tiene método abreviado, pero tampoco lo necesita:
x = ~x;
Como puedes observar, la operación es más o menos como las abreviadas anteriores.
¡No confundas los operadores bitwise con operadores booleanos!
Es muy fácil confundir el operador bitwise AND (&) con el operador de boleanos (&&). Ambos son diferentes por dos razones:
- No calculan los números del mismo modo, bitwise hace los cálculos bit a bit mientras que el operador booleano primero convierte ambos a boolean. Por ejemplo,
4 & 2 == 0porque 4 es 100 y 2 es 010, y ninguno de los bits es 1 en ambos. Sin embargo4 && 2 == true, ya que ambos números son distintos de 0 y por lo tanto son tratados como true. El equivalente seríatrue && true == true. - Los operadores bitwise evalúan los dos operandos antes de realizar la operación, mientras que los operadores boolean usan una evaluación llamada short-cut. Esto sólo importa si los operadores tienen efectos secundarios, como mostrar una salida y modificar el valor de algo en memoria. En el siguiente ejemplo:
int fred (int x)
{
Serial.print ("fred ");
Serial.println (x, DEC);
return x;
}
void setup()
{
Serial.begin (9600);
}
void loop()
{
delay(1000); // wait 1 second, so output is not flooded with serial data!
int x = fred(0) & fred(1);
}
El resultado de este programa será:
fred 0 fred 1
Esto es debido a que el operador bitwise evalua primero el resultado de ambos operandos. Si por el contrario, sustituimos el operador bitwise por uno boolean (&&), el resultado será el siguiente:
fred 0
Como puedes observar, la segunda función no ha sido ejecutada. Esto es debido a que el resultado de la función de la izquierda es false, por lo que no es necesario evaluar la función de la derecha ya que se sabe con certeza que el resultado de la operación será false.
Lo mismo pasa con el operador bitwise OR (|) y el operador boolean OR (||). En operador bitwise evaluará ambos operandos antes de realizar la operación, mientras que el operador boolean evaluará sólo el primero en el caso de que este ya sea true por la misma razón, el programa ya tendrá la certeza de que el resultado será true.
Ahorra memoria y optimiza la velocidad con operaciones bit a bit
Ahora que te he enseñado cómo funcionan las operaciones bitwise bit a bit, es hora de que te introduzca un poco en cómo te pueden ayudar. Empezaremos con algo fácil como ahorrar memoria en los booleans.
Ahorra memoria en los booleans
Algo muy interesante para ahorrar espacio de la tan preciada memoria RAM de nuestros microcontroladores, es convertir los booleans a bits. Un boolean es un variable que puede tener dos valores true y false, que es el equivalente a un bit, que puede tener un valor 0 o 1. la diferencia radica en que un bolean consume un byte de memoria (8 bits), mientras que un bit consume una octava parte. Por desgracia no se pueden usar los bits por separado y hay que juntar varios en bytes, por lo que esta medida de ahorro no nos sirve si tan sólo tenemos un boolean.
Por poner un ejemplo para que lo entiendas mejor:
bool led1 = true; bool led2 = false; bool led3 = true; bool led4 = false; bool led5 = false; bool led6 = true; bool led7 = false; bool led8 = true;
El tamaño de esta ristra de booleans será de 8 bytes. ¿Cómo podemos optimizarlo?, pues usando bits:
byte leds = B10100101;
Este ejemplo al contrario que el de los bolean, consumirá tan sólo 1 byte de memoria y contendrá los mismos datos, por lo que estaremos ahorrando una gran cantidad de memoria.
Seguramente te preguntarás: sí, muy bien, pero ¿cómo verifico el estado de cada boolean?. La respuesta es fácil, utilizando operadores bit a bit, tal y como aprendimos más arriba.
if (led4 == true)
{
// Cosas que hacer
}
Este ejemplo es el ejemplo simple que se usaría con los bolean, simplemente comparas si es true y actúas en consecuencia. En el ejemplo de arriba sería false, por lo que no haría nada.
Para los bits sería parecido, y para ello usaremos el operador bitwise AND:
if (leds & B00010000)
{
// Cosas que hacer
}
En este caso la comparativa bitwise sería B10100101 & B00010000, y siguiendo lo aprendido anteriormente nos daremos cuenta de que el resultado será 0, que es el equivalente a false.
Esto además nos permitirá verificar varios boolean de una vez en lugar de utilizando OR, por ejemplo:
if (led4 == true && led6 == true && led7 == true)
{
// Cosas que hacer
}
Sería de la siguiente manera con un operador bitwise:
if (leds & B00010110)
{
// Cosas que hacer
}
Si cualquiera de los bits de leds es 1, el resultado será distinto de 0 y por lo tanto dará true.
Mejora la velocidad de tus programas
Me gustaría poder entrar más en detalle acerca de cómo modificar los registros de Arduino, por lo que en este caso os pondré un ejemplo simple relacionado con las operaciones bit a bit, y no me centraré en explicarlo muy a fondo.
Supongamos que quieres configurar todos los pines digitales desde el 2 hasta el 13 como output. De una forma estándar, los activarías ejecutando el comando pinMode en cada pin ya sea uno a uno o con un loop:
void setup()
{
pinMode (2, OUTPUT);
pinMode (3, OUTPUT);
pinMode (4, OUTPUT);
pinMode (5, OUTPUT);
pinMode (6, OUTPUT);
pinMode (7, OUTPUT);
pinMode (8, OUTPUT);
pinMode (9, OUTPUT);
pinMode (10, OUTPUT);
pinMode (11, OUTPUT);
pinMode (12, OUTPUT);
pinMode (13, OUTPUT);
}
void setup()
{
for (int pin=2; pin <= 13; ++pin) {
pinMode (pin, OUTPUT);
}
}
Ambos métodos son igualmente válidos, pero tienen dos problemas: son lentos y consumen más memoria de programa. Para que te hagas una idea, el primer ejemplo usa 638 bytes de memoria de programa, y el segundo 576 bytes. Si, es mejor usar loops en lugar de hacerlo a mano uno a uno, pero es mucho mejor si utilizamos operadores bitwise y los registros de Arduino. Los dos ejemplos de arriba se podrían condensar en dos líneas:
void setup()
{
// pone el pin 1 (transmisión serial) y los pines 2..7 como OUTPUT,
// deja el pin 0 (recepción serial) como INPUT o dejará de funcionar
DDRD = B11111110; // pines digitales 7,6,5,4,3,2,1,0
// pone los pines 8..13 como OUTPUT...
DDRB = B00111111; // pines digitales -,-,13,12,11,10,9,8
}
El funcionamiento de este último ejemplo será el mismo que los ejemplos anteriores, pero a diferencia de estos, la ejecución de este código será más rápida y el setch de ejemplo ocupará tan sólo 452 bytes, ahorrando 186 bytes frente al método manual, y 124 bytes frente al método usando un loop. Obviamente en el tema de la velocidad se notará poco ya que se ejecuta una vez y al inicio, pero supongamos que haces un proyecto que tengas que cambiar los pines de 0 a 1 muchas veces por segundo. En este caso sí te beneficiarás del aumento de velocidad.
Como siempre, espero que os haya gustado y nos seguimos viendo por aquí. Un saludo.